Geometri, her ne kadar birçok öğrenci tarafından sevilmeyen bir ders olsa da, günlük hayatımızın en önemli parçalarından biri konumunda. Yunanca “Geo” (yer) ve “Metro” (ölçüm) kelimelerden türetilmiştir. Ünlü tarihçi ve yazar Herodot, geometrinin kesin olmamakla beraber çıkış yerinin Mısır olduğunu söylemiştir. 

Bu yazımızın konusu da, geometrinin önemli parçalarından biri olan eşkenar dörtgen. Elmas olarak da bilinen bu şekil, birçok önemli özelliğe sahip. Gelin hep beraber eşkenar dörtgen özellikleri, alan hesabı formülleri ve iç açıları ile ilgili daha fazla bilgi edinelim.

 Eşkenar dörtgen nedir?

Eşkenar Dörtgen, paralelkenarın özel bir durumudur. Bir eşkenar dörtgende yer alan karşıt kenarlar birbirine paraleldir ve karşıt açılar eşittir ve dolayısıyla bir paralelkenarın koşullarını karşılar. Ayrıca, eşkenar dörtgenin tüm kenarı eşit uzunluktadır ve köşegenler birbirini dik açıyla keser. Bir eşkenar dörtgen, tüm açılarının 90 derece olması durumunda kare olarak da adlandırılabilir. 

Yukarıdaki şekilde, AB, BC, CD ve AD’nin eşkenar dörtgenin kenarları ve AC ve BD’nin eşkenar dörtgenin köşegenleri olduğu bir ABCD eşkenar dörtgenini görebilirsiniz.

Kare bir eşkenar dörtgen midir?

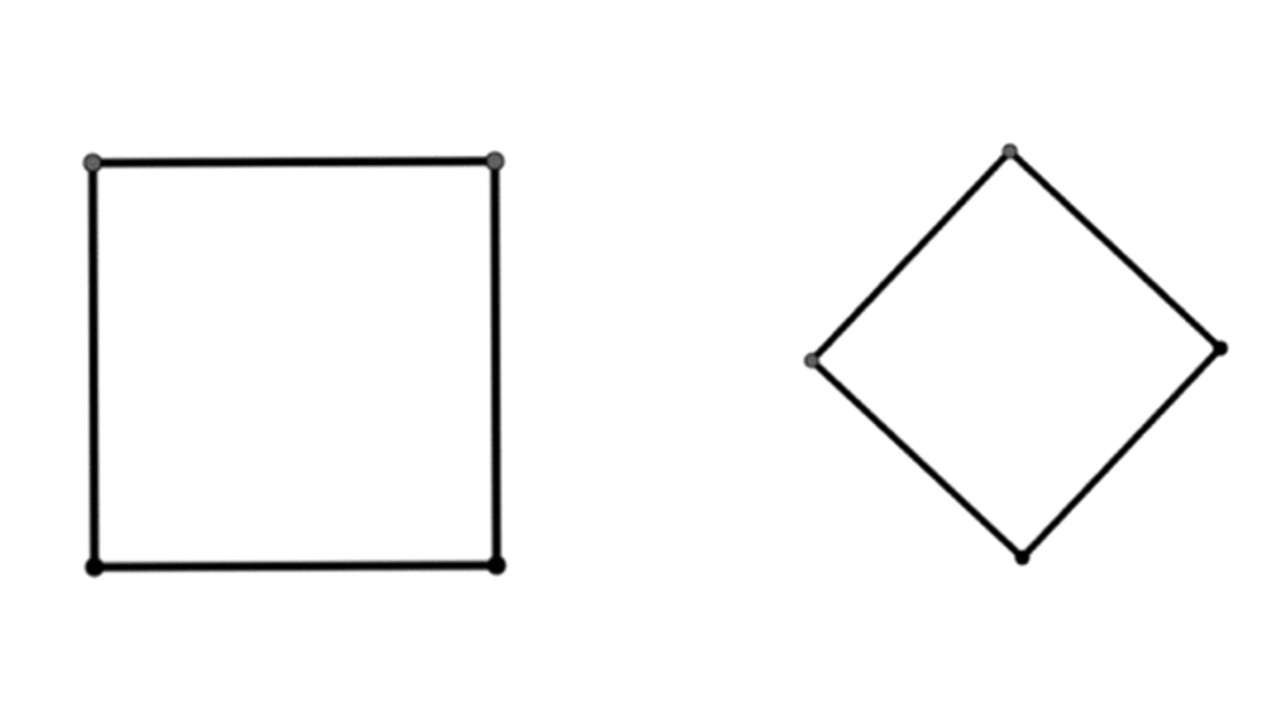
Kare ve eşkenar dörtgen bazı benzerliklere ve farklılıklara sahip. Hem eşkenar dörtgen hem de kare, paralelkenar olarak da adlandırıldıkları için benzer özelliklere sahip. Bir eşkenar dörtgende, eşkenar dörtgendeki zıt açıların bir çifti dardır ve diğer açılar geniştir. Ancak bu durum kare söz konusu olduğunda farklılık gösterir, çünkü dört açının her biri 90 derecedir. 

Bir karenin tüm kenarları eşit uzunlukta olduğundan dolayı, bir kare her zaman bir eşkenar dörtgen olarak sayılabilir. Buna ek olarak, hem karenin hem de eşkenar dörtgenin köşegenleri birbirine diktir ve zıt açıları ikiye böler. Dolayısıyla bir kare her zaman bir eşkenar dörtgen olarak da adlandırılabilir.

Eşkenar dörtgenin alanı nasıl hesaplanır?

• Yöntem #1: Köşegenleri kullanarak alan hesabı
• Yöntem #2: Tabanı ve yüksekliği kullanarak alan hesabı
• Yöntem #3: Trigonometri kullanarak alan hesabı (yani kenar ve açıyı kullanma)

• Adım #1: AC ve BD gibi iki köşegeni olan bir ABCD eşkenar dörtgenini ele alalım.
• Adım #2: Bir köşegeninin uzunluğunu bulun, Yani d1,  A ve C arasındaki mesafedir.
• Adım #3: İki köşegeninin uzunluğunu, yani B ile D arasındaki mesafe olan d2’yi bulun.
• Adım #4: Hem d1 hem de d2 köşegenlerini çarpın .
• Adım #5: Sonucu 2’ye bölün.
• Adım #6: Sonuç ABCD eşkenar dörtgeninin alanını verecektir.

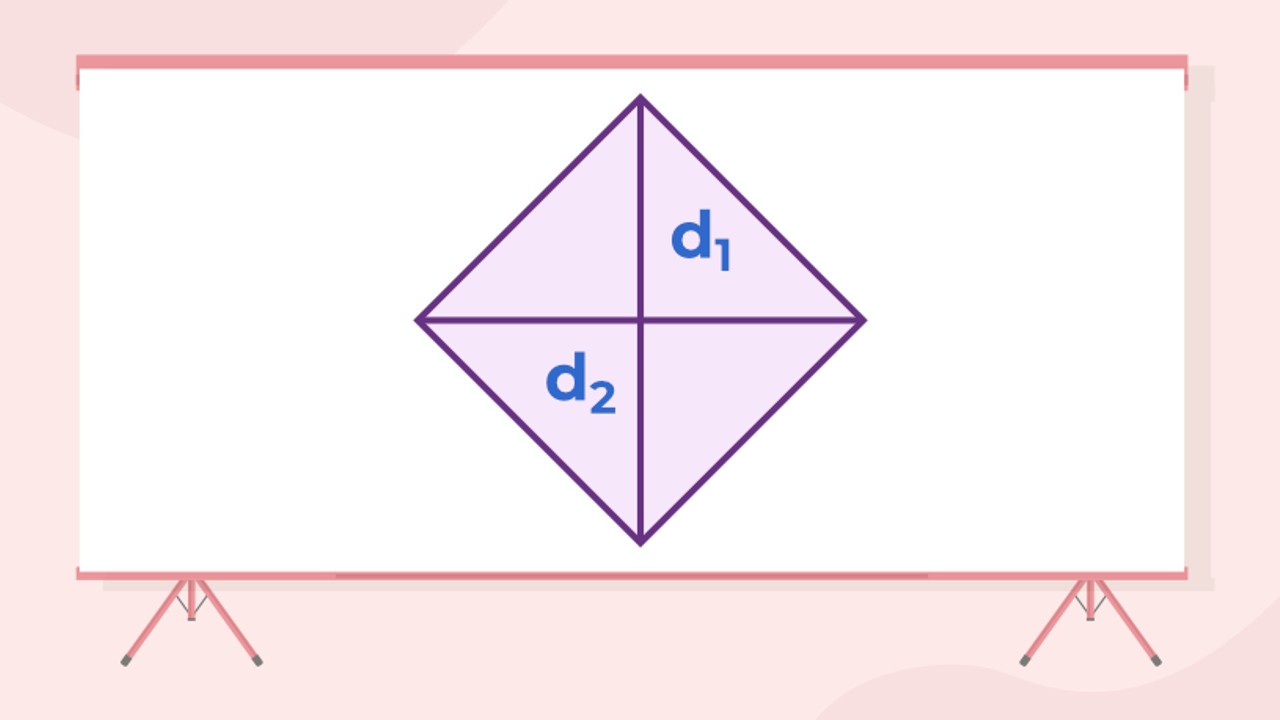
Köşegen uzunluklarını kullanarak eşkenar dörtgenin alanını hesaplamak için yukarıdaki adımları uygulamanız yeterli. Diğer hesaplama yöntemlerine göre biraz daha uzun olmasına rağmen, en sık kullanılan yöntemlerden biridir.

Örnek soru:

Köşegenleri 6 cm ve 8 cm olan eşkenar dörtgenin alanını hesaplayınız.

Çözüm:

d1 = 6 cm

d2 = 8 cm

Eşkenar dörtgenin alanı, A = (d 1 × d 2 ) / 2

= (6 × 8) / 2

= 48 / 2

= 24 cm2

Dolayısıyla eşkenar dörtgenin alanı 24 cm²’dir .

• Adım #1: Eşkenar dörtgenin taban ve yükseklik değerlerini verilen şekil üzerinden bulun ve hesaplayın.
• Adım #2: Tabanı ve hesaplanan yüksekliği çarpın.

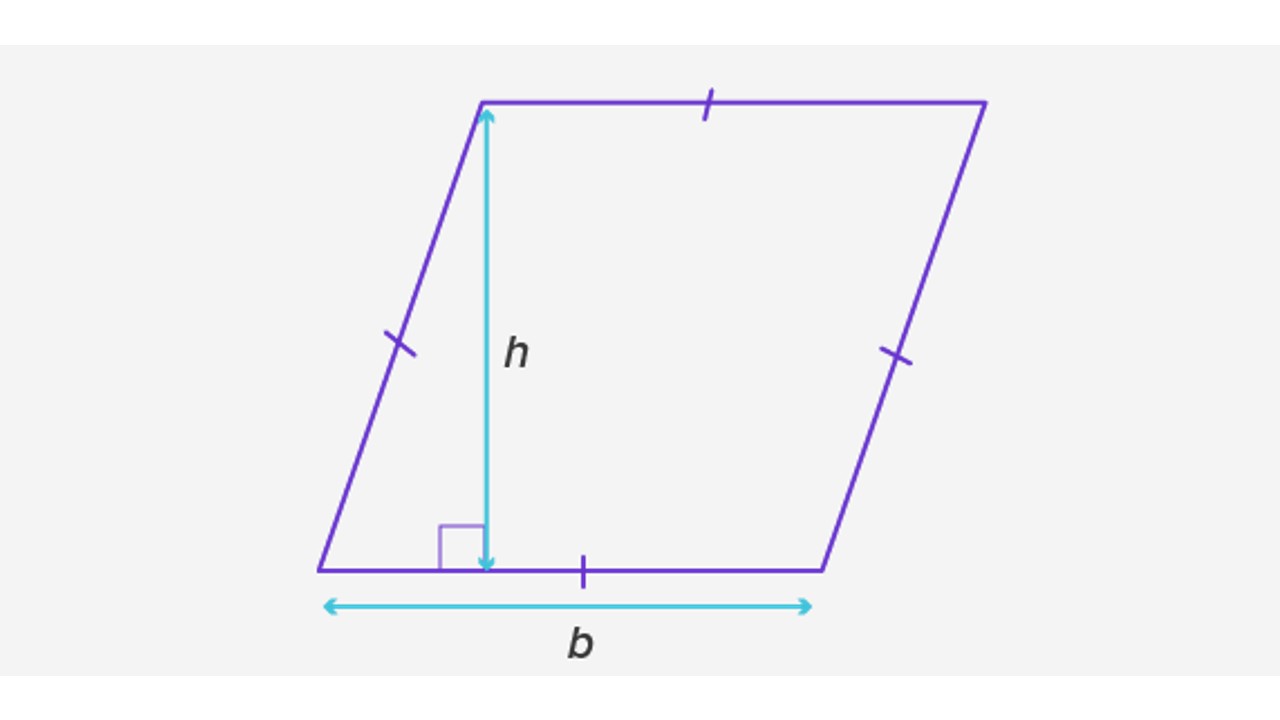
Eşkenar dörtgenin alanını hesaplamak için taban ve yüksekliği, yukarıdaki adımlarla beraber kullanabilirsiniz.

Örnek soru:

Tabanı 10 cm ve yüksekliği 7 cm olan eşkenar dörtgenin alanını hesaplayın.

Çözüm:

Taban, b = 10 cm

Yükseklik, h = 7 cm

Alan, A = b × h

= 10 × 7 cm²

A = 70 cm²

• Adım #1:  Eşkenar dörtgenin kenarlarından herhangi birinin uzunluğunun karesini alın.
• Adım #2: Açılardan birinin sinüs değeri ile çarpın.

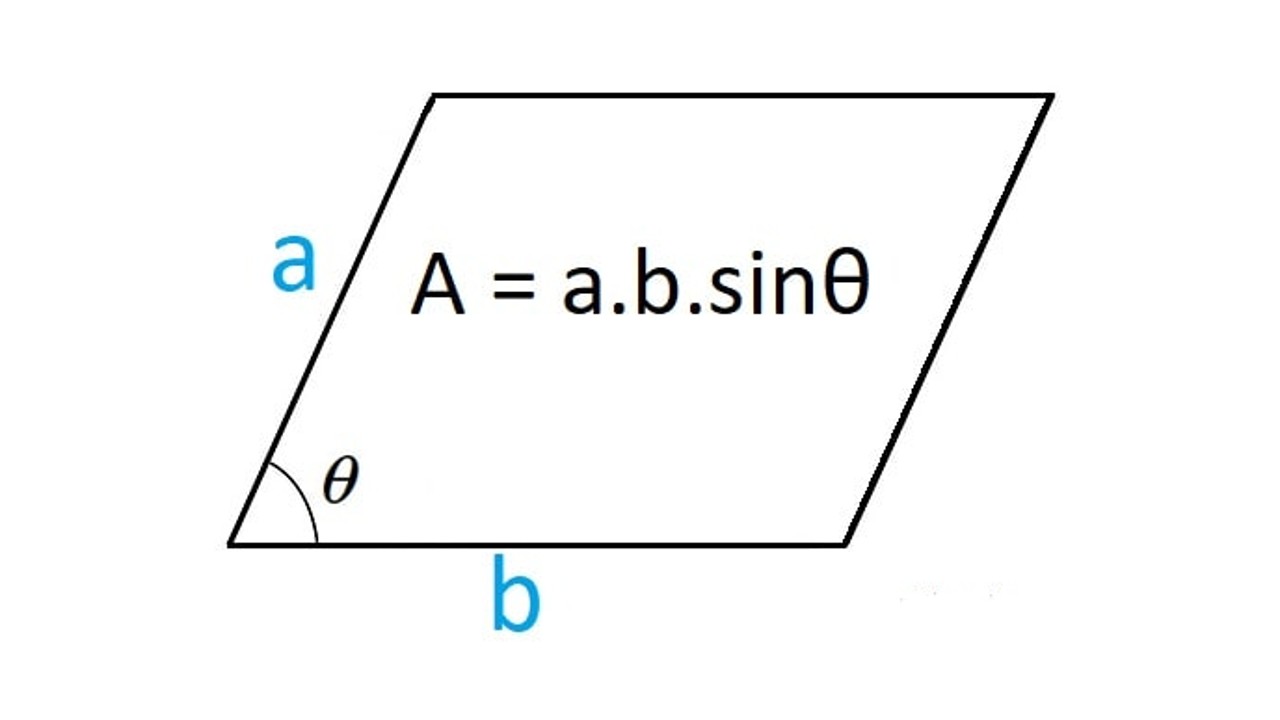
Eşkenar dörtgenin alanını hesaplamak için en az tercih edilen yöntemlerden olan biridir. Yukarıdaki adımları takip ederek, trigonometrik alan hesabı yapabilirsiniz.

Örnek soru:

Bir kenarının uzunluğu 2 cm ve A açılarından biri 30 derece olan eşkenar dörtgenin alanını hesaplayın.

Çözüm:

Kenar = s = 2 cm

A açısı = 30 derece

Kenar uzunluğunun karesi = 2 × 2 = 4

Alan, A = s² × sin (30 ° )

A = 4 × 1/2

A = 2 cm²

Eşkenar dörtgenin özellikleri:

• Karşı açılar birbirine eşittir
• Üç farklı isim ile anılırlar
• Köşegenler birbirini 90 dereceyle ortalar
• İç açılarının toplamı 360’tır.

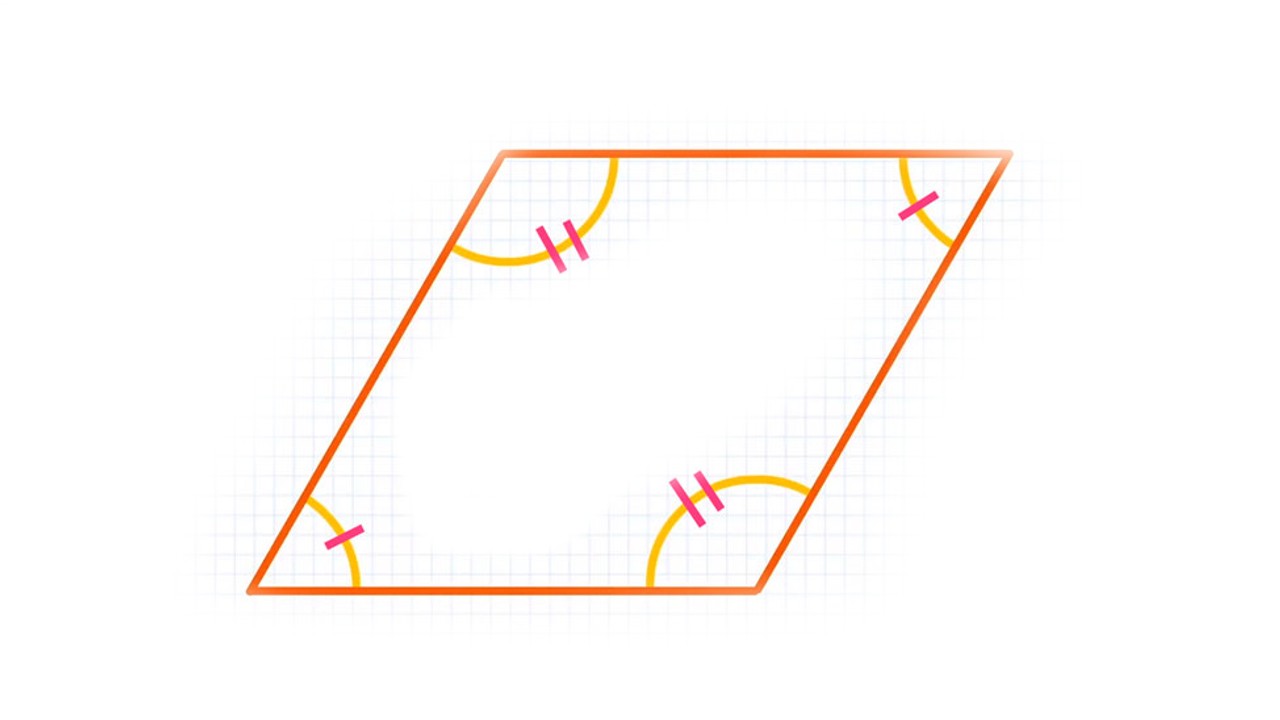
Eşkenar dörtgenin adından da anlaşılabileceği üzere dört iç açısı vardır. Karşıt köşeleri birleştirerek eşkenar dörtgenin içinde iki köşegen de oluşturabilirsiniz. Bu şekli düz bir yüzeyde nasıl düzenlerseniz düzenleyin, her zaman iki eşit zıt açıya sahip olduğunu görürsünüz.

Eşkenar dörtgen, görünüşü itibariyle günlük yaşamımızda karşımıza çıkabilecek birçok nesneye benziyor. Ancak genel olarak üç farklı isim ile anılırlar.

• Eşkenar dörtgen
• Pastil
• Elmas

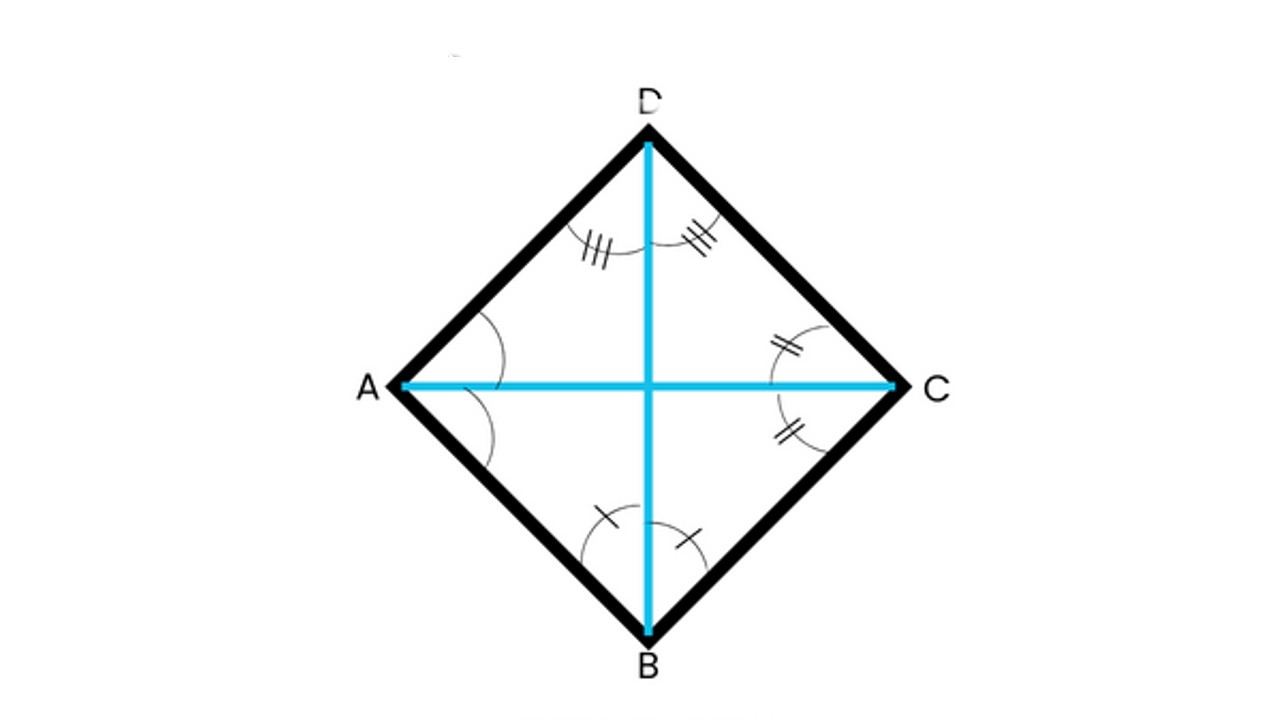
Eşkenar dörtgenin bir başka ilginç ve harika özelliği, köşegenlerinin her zaman birbirine dik olmasıdır. Hangi iç açılara sahip olursa olsun, eşkenar dörtgenin köşegenleri her zaman birbirine dik açıyla gelirler. Aynı zamanda bu köşegenler birbirini tam olarak iki eşit parçaya böler.

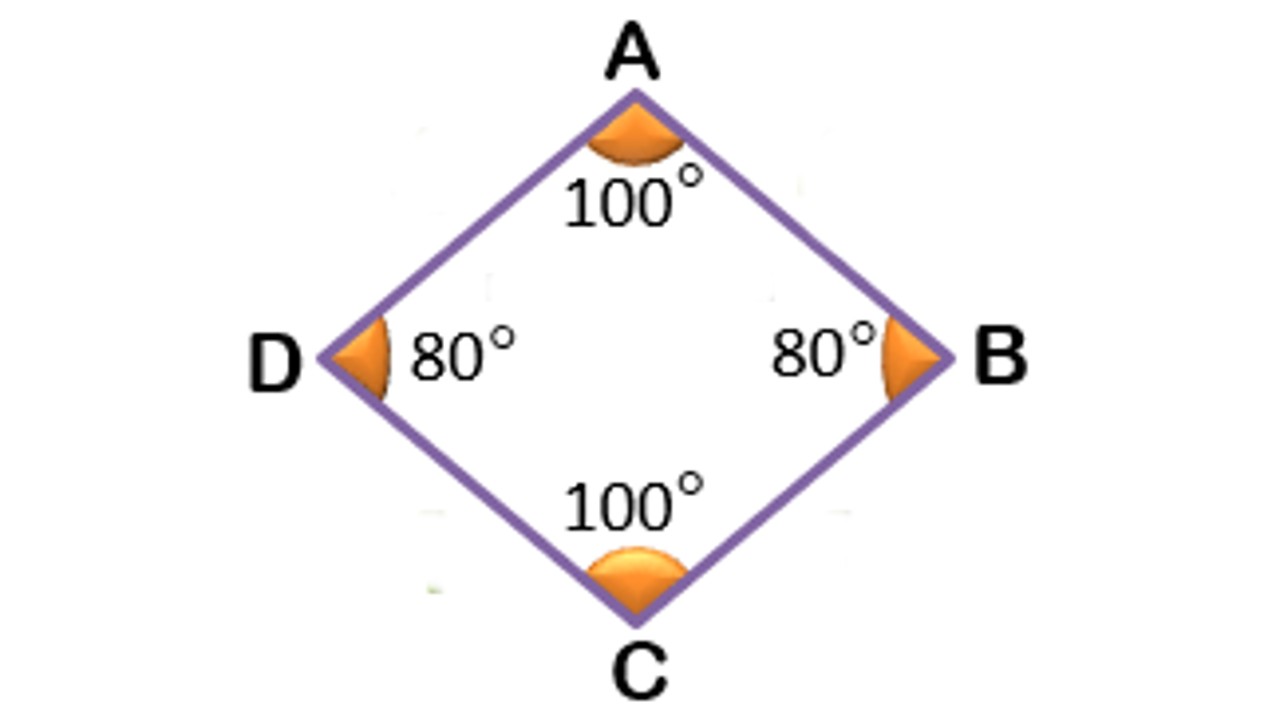
Yukarıda da bahsettiğimiz gibi, paralelkenarın özel bir durumu olarak da sayılan eşkenar dörtgenin köşegenleri onu 2 üçgene böler. Bildiğiniz üzere, bir üçgenin iç açıları toplamı 180 derecedir. Yani 2 üçgen oluştuğuna göre, iç açıları toplamının da 360 derece olduğunu görebiliriz.